Some of the algorithms are just outright likeable at first sight in their simplicity and effectiveness. Huffman coding is one of them for me.

We humans don't really like working with shifting 0 and 1 on a conscious level¹. We like to use characters to form a word, to convey meanings to one another. However, machines understand and store information as binaries, so we need a way to encode and decode text to binary codes.

Fixed-length binary codes

Naturally we can think the same number of bits to encode each symbol. For example, ASCII standard uses 7 bits to encode each symbol(character), therefore it is possible to encode 128 (2^7) unique values. But we could do better!

Variable-length binary codes

The key insight is that when some symbols occur much more frequently than others, variable-length codes can be more efficient than fixed length codes. That is, more common symbols can be represented using fewer bits than less common symbols. Therefore, best binary code for the job depends on the symbol frequencies.

But variable-length code comes with precautions - it can be unclear where one symbol starts and the next one begins. To remove this ambiguity, we should make it prefix-free.

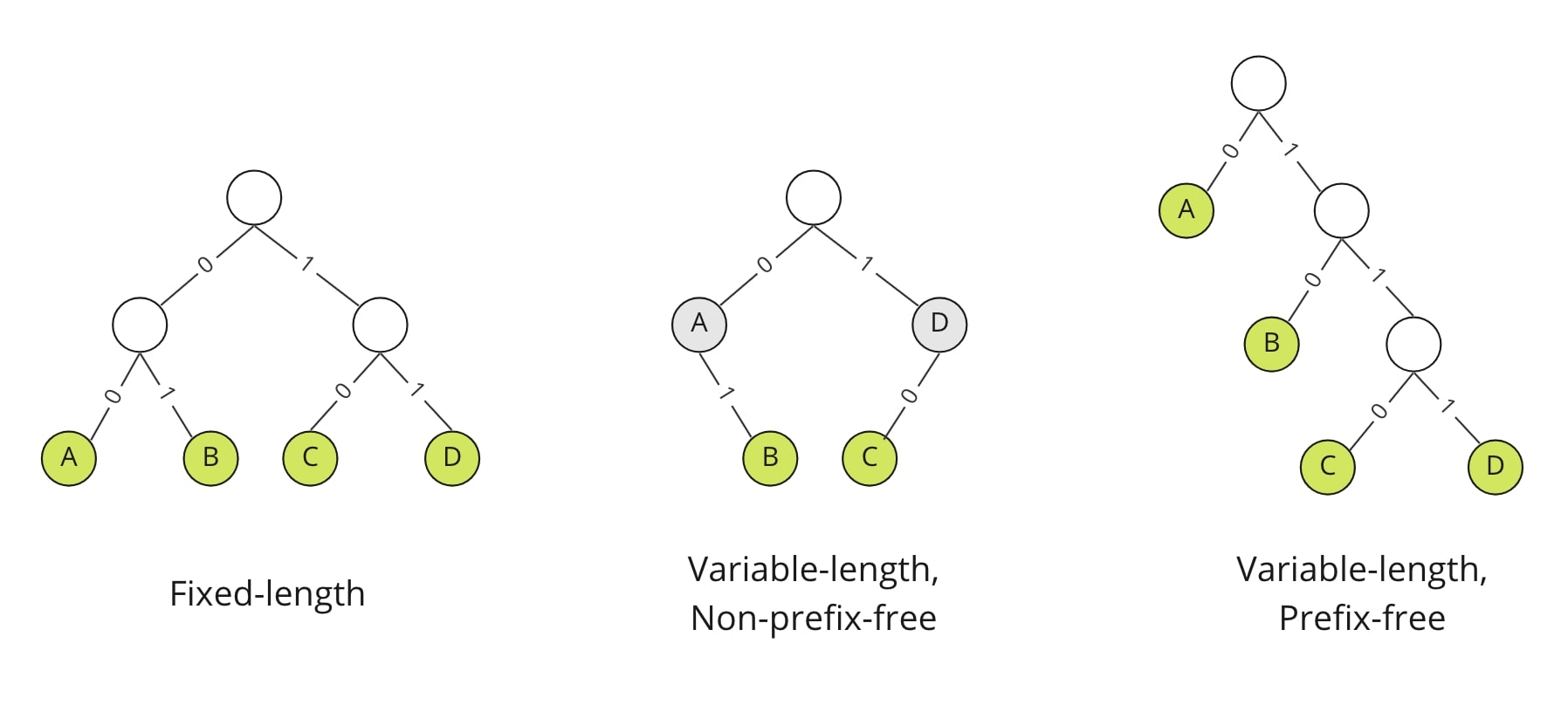
If we represent the codes as trees, we can see clearly what it would mean to be prefix-free. Here, every binary code can be represented as a binary tree with left and right child edges labeled with 0 and 1 respectively, and with each symbol as the label for exactly one node.

The encoding of a symbol 'a' is a prefix of that of another symbol 'b' if and only if the node labeled 'a' is an ancestor of the node labeled 'b'. Because no leaf can be the ancestor of another by definition, a tree with labels only at the leaves defines a prefix-free code.

Huffman’s greedy algorithm

This algorithm was developed in 1950s, and is still a widely used method for lossless compression².

We can tackle the optimal prefix-free code problem using a bottom-up approach. Start with N nodes each labeled with a different symbol of the set, and build up a tree through successive mergers. The algorithm maintains a forest, which is a collection of one or more binary trees. The objective function would be minimising the average leaf depth.

• Every iteration of Huffman’s greedy algorithm myopically performs the merge that least increases the objective function.
• Every iteration, it merges the two trees that have the smallest sums of corresponding symbol frequencies.
• Final encoding length of a symbol is precisely the number of mergers that its subtree has to endure. mergers increase the encoding length of the participating symbols by one.
• It is guaranteed to compute a prefix-free code with the minimum-possible average encoding length.

Time complexity of the Huffman algorithm is O(NlogN), and if the frequencies are already sorted, O(N).

---

1. I want to write about this - reminder for myself.
2. From Wikipedia: "Prefix codes nevertheless remain in wide use because of their simplicity, high speed, and lack of patent coverage. They are often used as a "back-end" to other compression methods. Deflate (PKZIP's algorithm) and multimedia codecs such as JPEG and MP3 have a front-end model and quantization followed by the use of prefix codes; these are often called "Huffman codes" even though most applications use pre-defined variable-length codes rather than codes designed using Huffman's algorithm."