Topological ordering

What does topology mean in the context of a graph?

It means an arrangement where the vertices are connected together.

What are the characteristics?

• All DAG(directed acyclic graph) has at least one topological ordering.
• Topological ordering is possible if and only if the graph has no directed cycles, i.e. if the graph is DAG.
• Topological orderings are NOT unique.

How do we compute topological ordering?

With DFS

We can obtain the topological ordering information from Depth-First Search (DFS) almost by default. In order to do so, we traverse the entire graph with DFS and record the finishing time of each node, adding it to the global ordering of nodes only after all of its children have been visited. To achieve this, we can use a stack data structure to store the vertices as they finish and then pop them out to generate a topological order.

Why would this produce topological ordering? Because when vertex v is finished, all the children vertices must have been ‘finished’ before v. And as we’re reversing the order according to finishing time, the ancestors (parents) come before the descendants (children).

With BFS (Kahn’s Algorithm)

Kahn's algorithm basically stems from Breath-First Search. In this approach, pay close attention to how we pick the vertices in the first place. We always pick the vertices that have no incoming edges and insert them into a queue. At least one such node must exist in DAG.

Computing Strongly Connected Components (Kosaraju’s algorithm)

What is a strongly connected component (SCC) of a directed graph?

It is a maximal subset of S ⊆ V of vertices such that there is a directed path from any vertex in S to any other vertex in S. Basically from any vertex you can reach any other vertex.

SCC Meta-graph is a directed acyclic graph.

This is actually the most fun insight. Every directed graph can be viewed as a DAG(directed acyclic graph) built up from its SCCs. Every directed graph can be viewed at two levels of granularity. Zooming out, you focus only on the acyclic relationships among its SCCs. Zooming in to a specific SCC reveals its fine-grained structure.

How can we learn about SCC structure? Our graph search algorithms can uncover SCCs, provided that we start from the right place. What is the ‘right place’? Intuitively, we want to discover a sink SCC, then work backward - i.e. We want to discover the SCCs in reverse topological order.

Kosaraju’s algorithm

1. Create G’ which is the input graph Q with every edge direction reversed.
2. Call DFS from G’, processed in arbitrary order to compute a finishing time f(v) for every vertex.
   • This is to identify the sink SCC in the original graph (source SCC in reversed graph)
3. Call DFS from every vertex of G, processed from highest to lowest finishing time, to compute the identity of each vertex’s strongly connected component.

Wait, why are we doing this funky business of reversing?

We observed that in DAG, the vertex finishing time made a topological ordering, and the last vertex in topological ordering (with no outgoing edges) belonged to a sink vertex. However, this does not hold true for the general directed graphs. Important insight though is that the vertex that comes first in topological order always belongs to the source SCC.

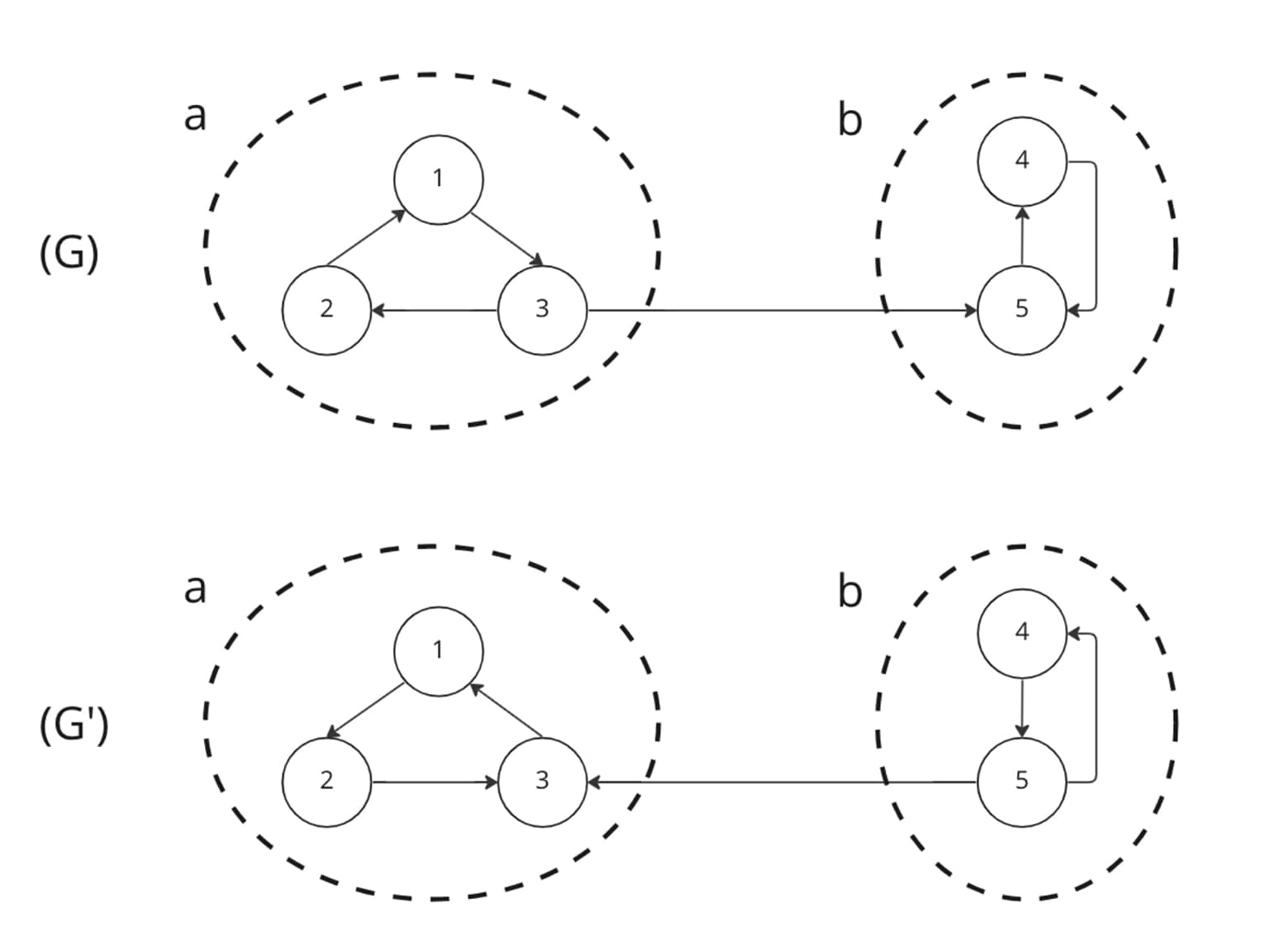
Why would that be true? Remember, the position in topological ordering is reversed order of the finishing time of a vertex in DFS.

On graph Q, imagine DFS searching in all cases:

• DFS started with vertex belonging to SCC a, for example, 2. DFS might finish vertex 2 before any of the vertices in SCC b, if it goes through (3,2) edge instead of (3,5). What’s guaranteed though, is that at least one of a’s vertices will be finished after all the vertices in SCC b (namely, 4 and 5) are finished, because SCC b are children of SCC a. Because we reverse finishing time to produce topological order, this vertex that finishes after SCC b will come before vertices in SCC b.
• DFS started with vertex belonging to SCC b, for example, 5. There is no outgoing edge from b to a, so all the vertices in b will finish first, and then we will process SCC a in the outer loop to call a new DFS. In this case, every vertex in a will have a topological position smaller than every vertex of b.

In conclusion, the vertex in the first position in topological order always belongs to a source SCC. after one pass of DFS, we can immediately identify a vertex in a source SCC. The only problem is that we want to identify a vertex in a sink SCC. What do we do? Reverse the graph!

Recall that zoomed out, SCC Meta-graph is a directed acyclic graph. Reversing the direction doesn’t really affect much on the SCC itself as the cyclic pocket will be unchanged, but it does reverse the direction of edges that connect SCCs. Therefore, reversing makes source SCCs into sink SCCs, and sink SCCs into source SCCs.

What’s left, then, is to pluck off the SCCs one by one on step 3.

---

Terminology

Edges in DFS forest

• Forward: an edge connecting a parent to one of the non-direct children in the DFS tree
• backward: an edge that is connecting one of the vertices to one of its parents in the DFS Tree
• cross: an edge connecting vertex from one of the DFS trees to another DFS tree
• tree: an edge that belongs to the main edges visited to make the DFS tree

This is explained well in this page and this page.

finishing time (exit time)

When all the children of vertex X are visited, we say the vertex is finished. The positions we get from topological ordering is acquired by reversing the finishing time ordering.

Incoming degree (indegree)

The number of incoming edges of the vertex

Outgoing degree(outdegree)

the number of outgoing edges of the vertex

sink SCC

SCC with no outgoing edges

source SCC

SCC with no incoming edges

transposed graph

Graph with reversed edges